Aufgabe B 2
Die Punkte A(6|6|0), B(2|8|0) und O(0|0|0) sind Eckpunkte einer dreiseitigen Pyramide mit der Spitze S(4|6|10).
Die Ebene E enthält die Punkte A, B und C(2|3|5).
a) Stellen Sie die Pyramide in einem geeigneten Koordinatensystem dar.
Bestimmen Sie eine Koordinatengleichung der Ebene E.
(Teilergebnis: E: x1+2x2+2x3=18)
(3 VP)
b) Zeigen Sie, dass das Dreieck ABC gleichschenklig ist.
Berechnen Sie das Volumen der Pyramide, die das Dreieck ABC als Grundfläche und den Punkt S als Spitze hat.
(4 VP)
c) In einem Koordinatensystem, bei dem die x1x2-Ebene den Erdboden beschreibt, stellt die Pyramide ABOS ein Kunstwerk dar (Koordinatenangaben in m).
An der Stelle, die durch den Punkt F(8|3|0) beschrieben wird, steht ein Mast senkrecht auf dem Erdboden. Auf den Mast treffendes Sonnenlicht lässt sich durch parallele Geraden mit dem Richtungsvektor
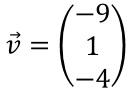beschreiben.Der Schattenpunkt der Mastspitze liegt auf der Kante des Kunstwerks, die durch die Strecke OS beschrieben wird.
Beschreiben Sie ein Verfahren, mit dem man die Höhe des Masts rechnerisch bestimmen kann.
(3 VP)
| Downloads |
PowerPoint